常见等价无穷小在线播放_常见等价无穷小替换公式(2024年11月免费观看)
湖南专升本数学143分备考攻略! š 打好基础 对于大多数零基础的同学来说,首先要巩固高中数学的基础知识。比如平方差公式、立方差公式、常见的乘除约分运算、指数函数运算、三角函数以及常见函数图像等。 ᠥš题技巧 别钻牛角尖!任何题型都不要想得太复杂,答案往往在题干中很明显。如果想到自己以前做过类似的题型,就用相同的解题方法做题。 先把24年的统考真题做三遍,很多知识点都是相通的,通过做题找到自己的薄弱点。 高数必考的函数有:幂函数、指数函数、对数函数、三角函数(背熟背烂!)。 求极限的题型:0:0型、∞:∞型等价无穷小还是抓大头,1的∞型第二重要极限。 不定积分的方法:根式换元、分部积分、凑微分法。 二重积分的题型:面积、体积、极坐标等。 无穷级数的样式:正向级数、交错级数、任意项级数、幂级数,不同级数不同符号样式。 备考方法 预习:课前预习很重要,先了解本节课的内容和重难点,这样上课听更有侧重点。 背公式:公式、定理、相应例题非常重要。很多题做不出来是因为找不到切入点,只有掌握例题的题眼——公式间的联系,做题才会更轻松。 听课:听课不要放在技巧上,主要是学思路,因为不是所有题都能让你“秒杀”。 刷题:基础课听完就该刷题了,直接刷模拟题,后期每天一套卷,抓自己的薄弱点和优势。错题要及时整理,每周考点尽量当天解决。 – 备考心得 基础薄弱的题型就往死里刷,基础不牢固别上去就刷套卷。 后期每周计时模拟一套卷,严格按照考场时间来,做完要对答案修改和复盘,把错题捋顺。 每天10极限+10求导+10积分题保持手感,不要做太难太偏的题,找些基础题训练计算能力和速度就好。 一定要给自己进步的过程,一轮做基础题,二轮上难度,三轮抓难题和技巧,把每一步走稳走扎实!
极限与无穷小:你真的觉得它们难吗? 你觉得极限和无穷小很难?其实,它们并没有你想象的那么复杂!ŽŒ握一些小技巧,你就能轻松搞定它们! “抓大放小”原则:这个方法特别适用于多项式函数的极限问题。当x趋于无穷大时,我们要关注最高次幂项,忽略低次幂项;而当x趋于0时,则要抓住最低次幂项,忽略高次幂项。这样,我们就能快速准确地求出极限值。 无穷小量的比较:在同一变化过程中,比较两个无穷小量趋于零的速度。阶数越高的无穷小量,其趋于零的速度就越快。因此,在解决相关问题时,我们需要熟练运用这一原理进行判断和分析。 等价无穷小:简单来说,就是在某些特定条件下,一些函数可以被近似成另一个更简单的函数,使得计算更加方便快捷。例如,当x趋近于0时,sin(x)就可以被近似成x。这就是所谓的等价无穷小替换。 使用方法:首先,我们需要记住一些常见的等价无穷小关系,例如ln(1+x)~x, (1+x)^a-1~ax等等。然后,在遇到复杂的极限问题时,我们可以利用这些关系来进行巧妙的变换,从而化繁为简,迅速得到答案。 注意事项:等价无穷小替换并不是万能的!在使用时要遵循一定的规则,比如在乘除法中可以随意替换,但在加减法中则需要谨慎处理。只有正确理解并灵活运用这些规则,才能真正发挥出等价无穷小的强大威力。
高等数学每日一题:等价无穷小详解 Ÿ 知识点:常见等价无穷小 š 每日一题 也许眼前充满各种苟且,但学习,是为了和远方的诗意相遇。 € 高等数学中,等价无穷小是一个非常重要的概念。以下是一些常见的等价无穷小表达式: 1️⃣ 当 x→0 时,x~sinx~tanx~arcsinx~arctanx~e⁻ln(1+x) 2️⃣ sinx-tanx~2(1+x)-1~ax, a-1~x^na (a>0), x-1n(1+x) 3️⃣ 1-cosx~2xⲊ4️⃣ x-arcsinx~x-sinx~x-tanx~x-arctanx 5️⃣ xⲾln(1+x) 6️⃣ x⳾ln(1+x) 7️⃣ x⁶~ln(1+x) 8️⃣ x⁶~ln(1+x) 9️⃣ x⁶~ln(1+x) Ÿ x⁶~ln(1+x) ᠨ🙤퉤— 穷小表达式在高等数学的解题中非常有用,掌握它们可以大大简化计算过程。
武老师强化课极限部分复盘总结 大家好,今天我们来复盘一下武老师的极限强化课,真的是收获满满!这次复盘分为五个部分,每一部分都有一些关键知识点和技巧,希望对大家有所帮助。 第三讲:洛必达法则与等价无穷小 š 常见的基本极限:首先,我们回顾了一些常见的基本极限,比如洛必达法则。这个法则在什么时候可以用呢?比如,在x→0的时候,x的高次和低次之间可以进行“取大头”。 等价无穷小的使用条件:等价无穷小在什么时候不能用呢?比如,在(x-sinx)/x和(x-sinx)/x^3中,前者可以直接用等价无穷小,而后者却不能。这是因为等价无穷小的使用条件比较复杂,需要根据具体情况来判断。 洛必达法则的使用:洛必达法则在什么情况下使用呢?如果导数不连续,还能用吗?其实,只要满足一定的条件,洛必达法则就可以使用。 泰勒展开:三角函数和e的指数函数的泰勒展开怎么写?有没有什么简易的记忆方法?比如,可以根据奇偶性来记忆。 夹逼定理与定积分:夹逼定理什么时候用?定积分的定义什么时候用?“可爱因子”又是什么?这些问题都需要大家去思考和掌握。 第四讲:1的无穷型极限与数列极限 ⊱的无穷型极限:什么是1的无穷型极限?它的三步走是什么意思?这个三步走是怎么进行推导的?做一下图4,看看能不能做出来吧。 数列极限的计算:对于一个n项连乘的数列极限,怎么计算呢?怎么样能把乘法变为加法?如果说是对它们进行求导呢? 第五讲:无穷小量阶的比较与连续性 无穷小量阶的比较:对于无穷小量阶的比较,有哪些常用的方法?常见的求极限,是不是类似于等价无穷小的求解呢?武老师有个简单求变上限积分无穷小阶的方法,是什么呢? 连续性的概念:连续是一个怎么样的概念呢?间断点是怎么进行分类的呢?为什么第一类间断点没有原函数呢? 介值定理:什么是介值定理?零点定理如何用它推导出来呢? 总结 通过这次复盘,大家应该对武老师的极限部分有了更深入的理解。希望这些知识点和技巧能帮助到大家在考试中取得更好的成绩。如果你有任何问题或需要进一步的解释,欢迎在评论区留言,我们会尽力解答。 再次感谢武老师的精彩讲解,希望大家都能从中受益!
š高等数学无穷小与无穷大详解笔记 – 无穷小与无穷大 无穷小定义:若函数f(x)在x趋近于某个值时,极限为0,则称f(x)是x的无穷小。 š 极限为零:这意味着函数值趋近于0,但并不意味着它是“极小的数”。 Œ 等价无穷小:当x趋近于某个值时,若f(x)与g(x)的极限相等,则称f(x)与g(x)是等价无穷小。 ˆ 无穷大定义:若函数f(x)在x趋近于某个值时,极限为无穷大,则称f(x)是x的无穷大。 — 关系:f(x)是x的无穷小,而g(x)是x的无穷大。 Œ 重要关系:若f(x)是x的无穷小,且g(x)是x的无穷大,则f(x)与g(x)的乘积为1。 – 等价无穷小 等价无穷小的形式:当x趋近于某个值时,f(x)与g(x)的关系为等价无穷小。 š 常见函数:如sin x, cos x, tan x, arcsin x, arccos x, arctan x等。 ˆ 无穷小的比较 设f(x)与g(x)是x的无穷小,且f(x)与h(x)也是x的无穷小。 š 若f(x)与g(x)是同阶无穷小,则它们的关系为o(1)。 Œ 若f(x)与g(x)是等价无穷小,则它们的关系为1。 – 总结 无穷小与无穷大的概念是高等数学中的重要部分。 š 通过这些定义和关系,可以更好地理解和解决各种数学问题。
法国工程师申请:学长分享笔试准备全攻略 今天我们邀请了小苏学长,他之前分享过工程师院校的申请经验和就读感受,这次他来聊聊他的笔试准备心得,大家记得收藏哦! ⏰ 什么时候开始准备? 学长建议,最好提前三个月或更长时间开始准备。这样可以有条不紊地进行基础巩固和针对性强化。 Œ 从哪些方面进行准备? ⭐️ 基础巩固:目标明确,循序渐进 ‰ 这个阶段的目标是在有限的时间内尽快回顾大纲内的知识点。以下是针对数学、物理和专业课的复习建议: Ÿ 数学 学长采取的做法是按照考研数学进行准备,迅速回顾高等数学、线性代数和概率论三个模块的知识点。重点放在基础概念、数学公式和解题思路,比如高等数学中的等价无穷小、基本积分公式、不定积分和定积分的求法、定积分的应用、求偏导,还有常见的微分方程的解法和空间解析几何中的数学概念。 线性代数中也有很多的概念和定理需要理解和记忆,比如矩阵可逆的条件、矩阵的秩、矩阵的特征值和特征向量。 最后是概率论的知识点,一些常见的公式比如期望、方差、协方差、相关系数、全概率公式、贝叶斯公式,常见分布及其概率分布/密度和分布函数、常见随机变量的期望和方差等。 总的来说,这一步耗时较多,但非常重要。回顾相应知识点后要及时进行习题训练,尽量减少“眼会手废”的情况。 Ÿ 物理 学长主要围绕力学和电磁学两个专题进行复习,使用的教材是大学物理的授课教材和一些网上搜集的补充资料。复习重心放在对基础公式、定理及常见解题思路的回顾,还有一些常见的应用场景。 比如力学中的动量定理、动量守恒定律、机械能守恒定律,电磁学中的电场强度的计算、高斯定理、电势的计算、场强和电势梯度的关系、常见的电容器、静电场的能量等。学长觉得物理知识点多且杂,出题角度也可能很刁钻,但作为基础巩固阶段,掌握基本的公式和一些经典的应用场景就可以算是完成小目标了。 Ÿ 专业课 这一部分的复习方法因人而异,取决于不同的专业、专业课的难度深度以及遗忘程度。学长采取的做法是:在快速回顾知识点后,在网上搜集英语和法语的教学资料,包括公开课视频、教材、文章等。这一步主要是为了熟悉各种专业名词的表达,在考场上或者和老师沟通时尽量减少因为听不懂和不会表达带来的困扰。 未完~
大一高数知识点全解析š 同学们,期末考试快到了,赶紧复习吧!高数可不是闹着玩的,挂了可就麻烦了。下面是我总结的大一高数上册知识点,希望能帮到你们。 第一章:函数与极限ˆ 函数的概念 函数的极限 求极限的方法 重要公式和等价无穷小 洛必达法则 利用导数定义求极限 利用定积分定义求极限 函数间断点的分类 闭区间上连续函数的性质 第二章:导数与微分 基本概念 求导公式 常见求导方法 复合函数求导法则 反函数求导法则 隐形函数求导法则 对数求导法则 求n阶导数 两个函数乘积的高阶导数公式 第三章:微分中值定理与导数应用 罗尔定理 拉格朗日中值定理 柯西中值定理 泰勒公式与估值求极限 常用公式和麦克劳林公式 导数的应用 极值判断方法 凹凸性与拐点 凹凸的定义 凹凸性的判定方法 拐点判定方法 希望这些知识点能帮到你们,期末考试加油!ꀀ
1^∞型极限的简易解法 š不定式极限的常见形式包括: 0/0型 ∞/∞型 0ⷢˆž型 1^∞型 0^0型 ∞^0型 ∞-∞型 (后五种形式可以通过变换转化为前两种) 1^∞型极限的计算方法: 凑e法:将表达式转化为lim(x→0)(1+x)^(1/x)的形式。 对数恒等式法:对幂指函数应用对数恒等式进行变形,然后利用洛必达法则、等价无穷小替换、拉格朗日中值定理或泰勒展开等方法进行计算。 œ三部曲”解法: 第一步:将原式改写为lim[1+x)]^x)的形式(熟练后,填空题可省略此步)。 第二步:计算lim[x)x)]=A(A为一个确定的值)。 第三步:最终结果为e^A。 通过这些方法,可以更简便地解决1^∞型极限的问题。
如何证明极限存在:多种方法总结 证明极限存在并求出极限值的方法有很多种,以下是一些常见的方法总结: š 夹逼准则 如果函数f(x)和g(x)在x趋近于某个值时,都被另一个函数h(x)夹在中间,那么f(x)和g(x)的极限存在且相等。 ˆ 洛必达法则 当0/0或∞/∞型极限存在时,可以使用洛必达法则。具体方法是求导后再求极限。 Š 上下极限法 通过上下极限的讨论,可以证明某些级数的收敛性。 ‘ Taylor公式 对于一些函数,可以使用Taylor公式进行展开,然后通过比较系数来证明极限存在。 œ 级数收敛法 对于一些级数,可以通过判断其收敛性来证明极限存在。例如,常见的级数有p级数和几何级数。 š 中值定理 使用Lagrange中值定理或Rolle定理来证明某些函数的极限存在。 Š 等价无穷小量替换 在x趋近于某个值时,使用等价无穷小量替换来简化计算并证明极限存在。 这些方法在数学分析和大数赛中都非常有用,大家可以根据具体情况选择合适的方法进行证明。
两个重要极限的证明与记忆技巧 在数学分析中,两个重要极限是必须牢记的基础知识。以下是对这两个极限的详细证明和记忆技巧,帮助你能够快速准确地应用它们。 第一重要极限 形式:$\lim_{x \to 0} \frac{\sin x}{x} = 1$ 证明:利用常见的等价无穷小公式,当$x \to 0$时,有$\sin x \sim x$,因此$\lim_{x \to 0} \frac{\sin x}{x} = \lim_{x \to 0} \frac{x}{x} = 1$。 记忆技巧:记住这个极限的形式,当你看到$\frac{\sin x}{x}$时,能够立刻想到结果为1。 第二重要极限 形式:$\lim_{x \to \infty} (1 + \frac{1}{x})^x = e$ 证明:利用幂级数转换和常见的等价无穷小公式,当$x \geq 0$时,有$(1 + x) \sim e^x$,因此$\lim_{x \to \infty} (1 + \frac{1}{x})^x = \lim_{x \to \infty} e^{\frac{x}{x}} = e$。 记忆技巧:记住这个极限的形式,当你看到$(1 + \frac{1}{x})^x$时,能够立刻想到结果为$e$。 总结 若极限形如$\frac{\sin x}{x}$且极限类型为“型”,可直接写成1。 若极限形如$(1 + \frac{1}{x})^x$且极限类型为“型”,可直接写成$e$。 通过这些记忆技巧和证明过程,你可以更好地理解和应用这两个重要极限,从而提高解题效率和准确性。
迷你小手工
蓝鲸有多长
都江堰是谁修建的
雅浚b3
安娜卡列尼娜作者
吃公鸡的禁忌
广西车牌
职业学校英语
印度高分电影
eos
傣族手抓饭
现代修仙
戗台
央求的近义词
香港电影明星
唐氏综合征长相
蒜苔怎么长出来的
草泥马之歌
jojo替身大全
呼唤的意思
腿英语怎么说
门锁怎么安装
推哥push
前仆后继读音
袜子的英语怎么读
宋小睿几岁
大观园全景图
独白是什么意思
竹子的资料
河南大学人事处
成都烂尾楼
伊读音
清脆的什么
厉声呵斥
厦门攻略
一个土一个屈
成就的近义词
拿破仑战争时间
辽和金是什么关系
鸡泽会谱
虞读音
731是什么意思
月亮发光的原理
头加一笔是什么字
日本预言
731是什么意思
雪姑娘
格温蜘蛛
西班牙在哪里
北大清华哪个好
张子枫新电影
古诗渔歌子
征兆是什么意思
崇宁通宝
组织文化名词解释
附和是什么意思
石油工业
逍遥二仙
嫩茎的读音
海地面积
章子怡身价
文松电影
夏季时间
饱和盐水
狸的读音
义是什么意思
奖掖后学
txl啥意思
农的成语
724厂
老赖什么意思
云南蘸水
手信是什么东西
蒜蓉小龙虾图片
周楠最后怎么样了
吃饭粤语怎么说
张爱玲怎么死的
好看的logo
辛弃疾作者简介
初霁什么意思
美酒聊共挥
和田县属于哪个市
四川话方言
怎么去掉分节符
沙雕动画
莫衷一是什么意思
女人一级片
周杰伦专辑封面
耕云种月
丽的繁体
启功
揭阳市是几线城市
汉朝一共多少年
黄果树瀑布介绍
手帐怎么画
青加定
tvb女明星
小马怎么画
明楼是什么电视剧
955工作制
名不虚传造句
牛肉饺子馅怎么调
知否分集剧情
下车引之的之
中考定向生
红鸾星动
皑皑是什么意思
三牲
来的拼音怎么写
矢志不渝读音
佳木斯多大
奶茶店排行榜
logo欣赏
洛阳小吃
槭树怎么读
避讳是什么意思
书桌英语怎么说
我的世界刷经验
深情男主
chess怎么读
游电影
妖怪漫画
黄粱一梦的故事
三民主义的意义
两弹一星元勋
绿色的鸟
蜀国被谁灭的
彩照是什么底色
宽阔近义词
神奇的艾琳
955工作制
带菊字的诗句
礼物英语怎么读
银河补习班票房
一睹为快的意思
口户犬怎么读
逼格是什么意思
乌镇在哪个城市
陆川站
豢养是什么意思
h2是什么气体
窜天猴读音
混沌十大顶级法则
超火的英文歌
散读音
火锅脑花要煮多久
聊斋三姐妹
黄马褂是什么意思
国企单位
权衡是什么意思
西游记歌曲白龙马
蜚蠊怎么读
龙洋身高
心有所属什么意思
郑州市区面积
演员黄曼
郑州旅游
自来水ph值
泰国cp
惰字组词
四大家族红楼梦
林青霞电影
全智贤的电影
雅安地震是哪一年
雷电的形成原理
甘露寺之变
刘德华粤语电影
无私奉献的近义词
宝可梦红宝石
手机如何跑分
取缔役岛耕作8
扬名立万结局
安逸近义词
三个字的动漫
独角鲸牙
南航a350
tiktok歌曲
好用的下载软件
李白出生地在哪里
鸽子吃什么粮食
歌坛天后
千古是什么意思
鲁山旅游景点大全
红外线智能止鼾器
暴龙哥
亲核加成
锐利的意思
畔是什么意思
斗鱼结局
毛阿敏近况
爱国的电影有哪些
超燃英文歌
抗氧化剂有哪些
卡纸手工制作
亩数怎么算
淄博美食
酒杯杯歌词
脸大怎么瘦脸
学富五车怎么读
缺口林凡
最新视频列表

【归纳总结】八个常用的等价无穷小哔哩哔哩bilibili

【微积分】必背!等价无穷小常用公式总结!注意事项分析!做题超好用!哔哩哔哩bilibili

微积分 极限基本概念 常用的几个简单等价无穷小介绍 西瓜视频

第18节|等价无穷小,你学会了吗?#高等数学 #高数基础知识 #专升本数学真题 #高考数学题型分析 #函数入门基础知识 抖音
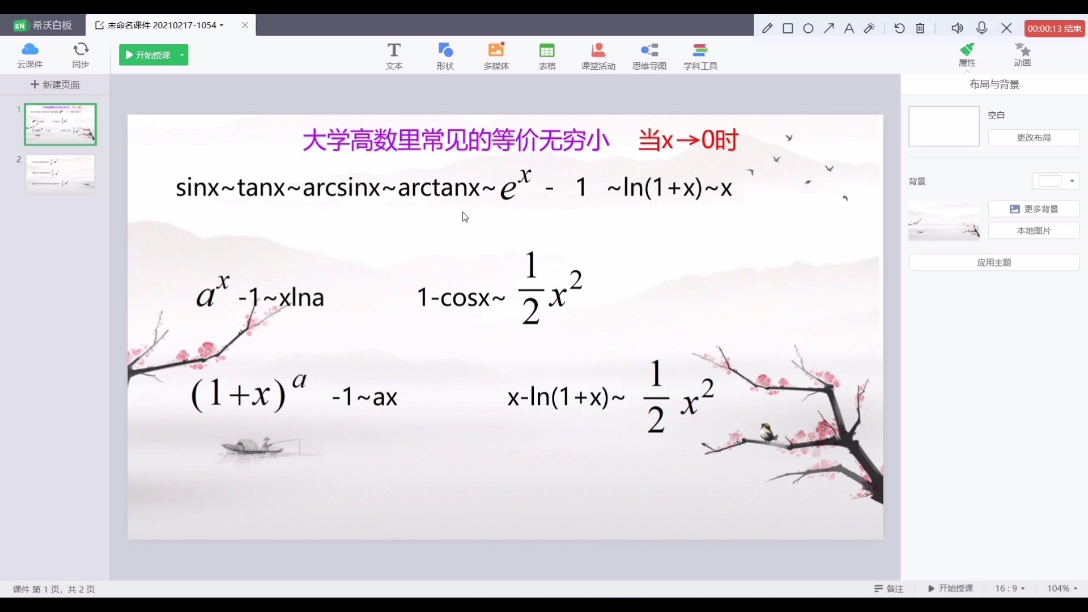
大学高数常见的等价无穷小哔哩哔哩bilibili

等价无穷小|同阶无穷小|高阶无穷小|低阶无穷小 相关概念? 解数学题的核心数学语言的转化哔哩哔哩bilibili

微积分:常用等价无穷小代换,为何没有单独COS等价的?

常用等价无穷小代换有哪几个?敲黑板:特别注意第五个!
最新素材列表
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
97都到强化轮了,还记不住公式,要不要硬记?
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
全网资源
相关内容推荐
专栏内容推荐
- 1080 x 1034 · png
- 高等数学中关于等价无穷小的一点思考 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 1112 x 1063 · png
- (等价无穷小与幂级数)泰勒公式_由泰勒公式推出的等价无穷小-CSDN博客
- 素材来自:blog.csdn.net
- 727 x 461 · png
- 常用等价无穷小公式是什么-百度经验
- 素材来自:jingyan.baidu.com
- 717 x 809 · jpeg
- 大一高数常用等价无穷小公式有哪些? - 知乎
- 素材来自:zhihu.com
- 828 x 745 · jpeg
- 等价无穷小常用替换公式? - 知乎
- 素材来自:zhihu.com
- 736 x 950 · jpeg
- 等价无穷小(常用)大全 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 600 x 983 · jpeg
- 等价无穷小(常用)大全 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 500 x 306 · jpeg
- 高等数学等价无穷小的几个常用公式
- 素材来自:wenwen.sogou.com
- 1231 x 1283 · jpeg
- 【数学荟萃】第3期:彻底讲清楚等价无穷小使用规则 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 素材来自:v.qq.com
- 788 x 757 · jpeg
- 同阶无穷小和等价无穷小的区别_初三网
- 素材来自:chusan.com
- 600 x 552 · jpeg
- 无穷小等价替换定理;用泰勒展开式推导等价无穷小公式 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 699 x 626 · jpeg
- 无穷小等价替换定理;用泰勒展开式推导等价无穷小公式 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 1600 x 893 · jpeg
- 常见等价无穷小的代换是什么-百度经验
- 素材来自:jingyan.baidu.com
- 716 x 723 · jpeg
- 有哪些常用的等价无穷小?? - 知乎
- 素材来自:zhihu.com
- 1080 x 810 · jpeg
- 高阶无穷小 ,低阶无穷小,同阶无穷小,等价无穷小 - 哔哩哔哩
- 素材来自:bilibili.com
- 474 x 355 · jpeg
- 等价无穷小公式 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 800 x 860 · png
- 等价无穷小符号
- 素材来自:zuowenzhai.com
- 1080 x 810 · jpeg
- 高阶无穷小 ,低阶无穷小,同阶无穷小,等价无穷小 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 素材来自:youtube.com
- 600 x 450 · jpeg
- 高阶无穷小 ,低阶无穷小,同阶无穷小,等价无穷小 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 300 x 424 · gif
- 常用等价无穷小等价替换-常见等价无穷小等价
- 素材来自:zhuangpeitu.com
- 550 x 403 · jpeg
- 常见的无穷小量、极限、等价 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 841 x 304 · png
- 高数常见坑点:等价无穷小 - 哔哩哔哩
- 素材来自:bilibili.com
- 646 x 452 · jpeg
- 无穷小等价替换定理;用泰勒展开式推导等价无穷小公式 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 600 x 699 · jpeg
- 【数学荟萃】第3期:彻底讲清楚等价无穷小使用规则 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 600 x 404 · jpeg
- 等价无穷小(常用)大全 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 600 x 924 · png
- 高数|第十回|无穷小的比较与等价无穷小
- 素材来自:sohu.com
- 2472 x 1126 · jpeg
- 大一高数常用等价无穷小公式有哪些? - 知乎
- 素材来自:zhihu.com
- 1491 x 380 · jpeg
- 搞定高数等价无穷小替换,这一篇就够了~ - 知乎
- 素材来自:zhuanlan.zhihu.com
- 397 x 65 · jpeg
- 高等数学等价无穷小的几个常用公式
- 素材来自:wenwen.sogou.com
- 480 x 78 · png
- 大一高数常用等价无穷小公式有哪些? - 知乎
- 素材来自:zhihu.com
- 755 x 205 · jpeg
- 常见的无穷小量、极限、等价 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 720 x 540 · jpeg
- 常见的无穷小量、极限、等价 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 600 x 143 · jpeg
- 【插班生/考研】高等数学每日一题(3)等价无穷小 - 知乎
- 素材来自:zhuanlan.zhihu.com
随机内容推荐
违章作业
北阿坎德邦
福鼎白茶图片
泸沽湖简介
知识的定义
斋藤飞鸟写真
怎么画青蛙
pdf编辑在线
交易费用理论
辅助光
战斗机怎么叠
巫净琥珀
王猎
博塔
宫颈位置图片
怎么投诉驾校教练
武夷岩茶水仙
登封嵩山
定海区政府
scac
剪辑视频怎么剪
猫纹
数学元素
做最坏的打算
就去涩涩
未来城市简笔画
bit和byte
舍之道
年金系数表
性虐网
庆祝生日
记忆T细胞
矩阵乘矩阵
好签
大计基
护士的图片
表白贺卡
今日头条平台
广西永福县
崇廉拒腐
防静电涂料
低耦合高内聚
波力海苔广告词
武修
哈尔滨市是哪个省
看电影的好处
验工计价
mcnp
动物组织
花字诗句
书法资料
亚寒带
陈姓的由来
明灭元
女生裸奔
lambda函数
起床啦表情包
管理学教材
幂次数列
喷塑工艺流程
整体结构
潘多拉的故事
运动方程
乐摄图
蝶豆
葫芦图案
强密码
金桥学校
赶英超美
鲍文卿
三上悠亚ssni
挂载点
棋盘覆盖问题
法国禁忌
cmd打开文件
章鲨2
皮皮虾去水印
舍之道
四年级生字表
susar
废标是什么意思
江苏无锡市
画杨桃课文
博润集团
宏观和微观
学位排名
性格优点
安全b证怎么考
一杯牛奶的故事
一计害三贤
建筑立面设计
农夫与蛇原文
画跑车
研讨交流
tanto
茶轴键盘
igf1
濮阳是哪里
班徽怎么设计
nh969
格子里的夜晚
如何画兔子
准备转变
泡罩
次数分布表
绞刑架图片
chobani
洛基电影
数字推理题技巧
汉景帝阳陵博物院
肝弹
基础形式
ak101
中国画分类
中华姓氏
院子图片
积极向上的书
三方国界
管理技术
orvibo
性虐网站
苦笋帖
中温带
小说虐恋
面试评价表模板
幼儿园汉字
闻一多代表作
diff函数
经济学基础知识
四世同堂话剧
李明昊
水化反应
简笔画人头
谐响应分析
草原白
贝云
甜甜的肉文
竣工备案表
氟碳面漆
卡地亚标志
仓鼠饲养八大禁忌
亚洲无线
x15
跳高图片
周冬雨排列
tcl脚本
节约时间
猎捕纪录片
js箭头函数
帕拉梅拉内饰
重装战姬
世界十大名人
壳体结构
mdsc
ejmc
亢奋美剧
c4d场景
世界地图大全
妲己新皮肤
idea打包
鸡首壶
起床啦表情包
老年综合评估
辩证唯心主义
社团组织
痘痘照片
产品理念
2018金马奖
日出日落图片
圣龙集团
书写的重要性
帝银事件
云网融合
泰山天外村
极品露出
末世小说女主文
表水是什么意思
单体单元
男人把女人
财务绩效
漫画是什么
战争和战略问题
世界史时间轴
干声
人甲骨文
家里来猫
形容人的形容词
颏肌
白胡椒粒
小跳蚤
德州农商银行
罪人电影
均值公式
经营资质
word添加批注
自制猫抓板
英文我爱你
如懿传好看吗
短横的写法
一味神药治痔疮
今日热点推荐
外交部回应优衣库不用新疆棉
安以轩老公被判处13年有期徒刑
第11批志愿军烈士安葬祭文
我是刑警 打码
印政府还在用被封杀4年的中国APP
巴黎世家售出8天后要顾客补1147元
蛇年春晚标识有什么寓意
韩安冉称do脸模板是赵露思
新疆棉是世界最好棉花之一
韩国人的精致穷
fromis9解散
鹿晗好拽
周密 格局
春晚官博回复檀健次春晚相关
这些抗老猛药敏感肌别碰
关晓彤迪拜vlog
我是刑警口碑
马云现身阿里巴巴园区
雷霆vs湖人
iQOONeo10打游戏包稳的
周密把周芯竹买话筒的钱转给她了
鹿晗回应喝多了
林志玲晒亲子照
导致胃癌的6个高危因素
TES官宣369续约
官方公布冷藏车厢内8人窒息死亡详情
中国游客在马尔代夫潜水遭鲨鱼咬头
樊振东回上海交大啦
油腻的小学生作文究竟是谁的错
张婧仪眉骨阴影
348万买的学区房厨房竟是违建
17名男女KTV聚众吸毒被一锅端
蛇年春晚官宣
iQOONeo10价格
宁悦一段演讲全是讽刺
再见爱人4第七期视频没了
杨紫 家业路透
iQOONeo10双芯战神
迪丽热巴ELLE2025开年刊封面预告
女子在中医诊所遭性侵医生被刑拘
祝绪丹 虞书欣丁禹兮的cp保安
fromis9合约到期不续约
安以轩得知老公被判13年后很伤心
王楚钦林诗栋赛前对练
冯绍峰接想想放学回家
纯白无瑕的新疆棉花不容抹黑玷污
冻掉手脚的志愿军战士遗憾没能冲锋
黄雅琼回应郑思维退出国际赛场
中俄在日本海空域战略巡航照片
声生不息等了卫兰三年
【版权声明】内容转摘请注明来源:http://kmpower.cn/zr98ep_20241127 本文标题:《常见等价无穷小在线播放_常见等价无穷小替换公式(2024年11月免费观看)》
本站禁止使用代理访问,建议使用真实IP访问当前页面。
当前用户设备IP:18.225.254.81
当前用户设备UA:Mozilla/5.0 AppleWebKit/537.36 (KHTML, like Gecko; compatible; ClaudeBot/1.0; +claudebot@anthropic.com)



























































