连续可微最新视觉报道_函数连续和可微的关系(2024年11月全程跟踪)
山东大学泰山学堂数学方向保研攻略 š 山东大学泰山学堂数学方向提供两次考试机会,不限原专业! „ 第一次考试在军训期间,主要考察高中数学知识。 š 第二次考试在大一上学期结束后,主要考察高等数学知识。 考试范围广泛,涵盖数学分析、高等数学等多个领域。 ᠧ‰᥈’包括: 判断命题是否正确,并证明或举反例。 证明存在满足特定条件的点列。 求极限和微分方程的解。 证明函数的一阶连续可微性。 讨论Riemann函数的连续性。 想要了解更多关于泰山学堂的特色培养和考试内容,欢迎咨询!
高数中连续、可导、可微的关系解析 在高等数学中,连续、可导和可微是三个非常重要的概念。它们之间的关系错综复杂,但也有一定的规律可循。下面我们来详细探讨一下这三个概念之间的关系。 连续与可微的关系 𑊊首先,连续和可微之间有着密切的联系。在一元函数中,可微函数一定是连续的。这是因为可微意味着函数的增量可以表示为自变量增量的线性主部加上高阶无穷小。具体来说,如果函数可微,那么当自变量增量趋近于0时,函数的增量也趋近于0,这正好满足连续的定义。 然而,连续函数不一定可微。例如,一些连续但不可导的函数自然也不可微。所以,连续是可微的必要条件,但不是充分条件。 可导与可微的关系 € 在一元函数中,可导和可微是等价的。如果函数可微,那么它的增量可以表示为自变量增量的线性主部加上高阶无穷小。当这个线性主部的系数趋于0时,函数在该点可导。反之,如果函数可导,那么它的增量也可以表示为自变量增量的线性主部加上高阶无穷小,这正好符合可微的定义。 多元函数中的关系 在多元函数中,连续、可导和可微的关系变得更加复杂。首先,连续和可导(偏导数存在)之间没有必然的联系。例如,函数f(x, y) = y^2在点(0, 0)处极限不存在,不连续,但在该点两个偏导数都存在。 多元函数中,可微一定连续。如果函数可微,那么它的全增量可以表示为自变量增量的线性主部加上高阶无穷小,这表明函数在该点的变化是连续的。然而,连续函数不一定可微。例如,函数f(x, y) = y^2在点(0, 0)处两个偏导数都存在,但函数在该点不可微。 偏导数连续与可微的关系 „ 在多元函数中,函数某点的偏导数连续,则必然可微。这是因为偏导数连续意味着函数在该点的变化是连续的,而这正是可微的定义。所以,偏导数连续是可微的一个充分条件。 具体例子分析 𐊊例如,函数f(x, y) = x^2 + y^2在点(0, 0)处连续,但不可微。这是因为当沿y = k趋近于(0, 0)时,函数的极限值与k有关,所以函数在(0, 0)处极限不存在,不连续。又因为f(x, 0) - f(0, 0) = x^2 - 0 = x^2,所以函数在(0, 0)处偏导数存在。 另一个例子是函数f(x, y) = x^2 + y^2在点(0, 0)处两个偏导数都存在,但函数在该点不可微。这是因为当沿y = k趋近于(0, 0)时,函数的极限值与k有关,所以函数在(0, 0)处极限不存在,不连续。 总结 总的来说,连续、可导和可微是三个相互关联但又有所区别的概念。在一元函数中,可微一定连续,但连续不一定可微;而在多元函数中,情况变得更加复杂。无论是在一元还是多元函数中,偏导数连续都是可微的一个充分条件。希望这篇文章能帮助你更好地理解这些概念之间的关系。
考研数学二元函数概念全解析 在考研数学的复习中,二元函数的相关概念是重点之一。以下是对这些概念的详细梳理和总结: 1️⃣ 二重极限 二重极限是二元函数连续性和偏导数存在的基础。 2️⃣ 二元函数连续 二元函数连续是指函数在定义域内任意两点间的值变化不大。 3️⃣ 偏导数存在 偏导数存在意味着函数在某一点处沿某一方向的变化率存在。 4️⃣ 偏导数连续 偏导数连续是指函数在某一点处的偏导数存在且连续。 5️⃣ 二元函数可微 二元函数可微是指函数在定义域内任意两点间的变化可以用线性函数近似。 考研数学二元函数相关概念关系总结: 1️⃣ 二元函数连续与偏导数存在的关系 连续函数不一定偏导数存在,但偏导数存在的函数一定是连续的。 2️⃣ 二元函数偏导数与可微的关系 偏导数存在的函数不一定可微,但可微的函数偏导数一定存在。 3️⃣ 二元函数可微与连续的关系 可微函数一定是连续的,但连续函数不一定可微。 4️⃣ 二元函数二阶偏导数与其他概念的关系 二阶偏导数存在是偏导数连续的基础,而偏导数连续又是可微的必要条件。 通过这些关系的梳理,可以更好地理解和掌握二元函数的相关概念,为考研数学打下坚实的基础。
”可微与偏导数连续的关系 你是否疑惑过,一个函数可微是否就能推出其偏导数连续呢?让我们一起来探讨这个问题吧! ˜首先,我们要明确什么是可微。可微,即函数在某一点处的全微分存在,这通常意味着函数在该点处的变化率是存在的。而全微分,对于二元函数来说,其实就是对两个自变量分别求偏导数,然后相加。 ”那么,可微与偏导数连续的关系是什么呢?其实,可微并不一定能推出偏导数连续。因为偏导数不连续,函数也可能仍然可微。这是因为,函数在某一点处的全微分存在,并不要求其偏导数在所有方向上都连续。只要函数在某个方向上的变化率存在,并且这个变化率与自变量的增量之比满足一定的极限关系,那么函数在该点就是可微的。 €以,我们不能仅仅因为一个函数可微,就断定其偏导数一定连续。这是一个常见的误区哦! ᦀ“一下,可微与偏导数连续的关系并不是简单的等同关系。函数可微,并不意味着其偏导数一定连续;反之,偏导数连续也并不一定意味着函数可微。我们需要根据函数的实际情况来判断哦!
”可微与偏导数连续的关系” 褽 是否在疑惑,如果一个函数可微,那么它的偏导数是否一定连续呢?”让我们来探讨一下这个重要的数学问题。 首先,我们要明确什么是可微和偏导数连续。可微是指函数在某一点附近的变化趋势可以用一个线性函数来近似,而偏导数连续则是指函数在某一点的偏导数存在且在该点附近的值变化趋势平稳。 ᧻过深入分析,我们发现可微并不一定能推出偏导数连续。虽然可微性是偏导数存在的一个充分条件,但并非必要条件。也就是说,存在一些可微函数,其偏导数并不连续。 因此,我们不能仅仅依据函数的可微性来判断其偏导数的连续性。在实际应用中,我们需要结合具体的函数形式和性质来进行综合判断。 ꥸŒ望这个解答能够帮助你更好地理解可微与偏导数连续之间的关系!如果你还有其他问题,欢迎随时提问哦!Š
多元函数可微、连续与偏导数的关系 在多元函数的概念题中,常见的有关于多元函数连续、偏导数存在问题、可微以及偏导数连续的推导。 首先,偏导数连续是最强的条件,可以推导出上述所有结论。 其次,可微的概念可以简单地理解为每个方向的导数都存在。既然每个方向的导数都存在,那么必然可以推出连续性。 再者,可偏导或可导在多元微分中指的是x和y方向的导数存在。因此,可微意味着每个方向的导数都存在,这自然可以推出x和y方向的导数也存在。所以,可微可以推出可导,或者可微可以推出可偏导。 最后,连续性和可偏导性没有直接关系。可偏导性指的是x和y方向的导数存在,但不能保证其他方向。然而,可偏导性可以推出x和y方向是连续的。
专升本高等数学知识点全解析 “ 专升本高等数学知识点归纳总结,助你轻松备考! š 第一讲:极限与连续 数列与函数 类型:初等函数、分段函数、复合函数、隐式函数、参数方程、变限积分函数、级数和函数等。 特征:单调性与有界性、奇偶性与周期性。 反函数与直接函数:y = f(x) → x = f(y) → y = f(x)。 极限性质 类型:无穷小与无穷大、未定型。 性质:有界性、保号性、归并性。 常用结论 等价无穷小:当u(x) → 0时,sin u(x) - u(x)、tan u(x) - u(x)、e - 1 - u(x)、ln(1 + u(x)) - u(x)等。 泰勒公式:e = 1 + x + x^2/2 + ...,ln(1 + x) = x - x^2/2 + ...,sin x = x - x^3/6 + ...,cos x = 1 - x^2/2 + ...。 常规方法 抓大弃小、无穷小与有界量积、洛必达法则、等价无穷小替换、泰勒公式处理等。 š 第二讲:导数及应用(一元) 基本概念 可导与连续:在x = 0处,连续但不可导;可导但不一定连续。 微分与导数:可微可导;比较“0”与“4”的大小。 求导准备 基本初等函数求导公式。 法则:四则运算、复合法则、反函数求导。 各类求导方法 定积分与不定积分、初等导数公式加法则、隐式函数求导存在定理。 š 第三讲:导数及应用(多元) 基本概念 偏导数与全导数:偏导数存在不一定全导数存在。 多元函数的极值:拉格朗日乘数法、约束条件下的极值问题。 常见应用 无穷小比较(等价,阶):f(x) - kx^n,(x → 0)。 渐近线(含斜率):渐近线方程的求解。 连续性:间断点判别、分段函数连续性。 š 第四讲:积分与微分方程 不定积分与定积分:不定积分的求解、定积分的性质与计算。 微分方程:一阶微分方程的解法、高阶微分方程的解法。 常见应用 面积与体积的计算:利用定积分求解面积和体积。 物理问题:利用微分方程解决物理问题。 ⛑️
”可微与偏导数连续的关系 在多元微分学中,有一个常见的问题:可微是否可以推出偏导数连续呢? ✅️首先,我们要明确,可微与可导、连续之间的关系并非简单的互推关系。 具体来说,连续并不一定能推出可微,但可微却可以推出连续。 𗢀♂️那么,对于偏导数呢? ž际上,可微可以推出偏导数的存在,但并不意味着偏导数一定是连续的。 𘥏,一阶偏导数的连续性并不能推出可微。 黎€以,当我们谈论可微与偏导数连续的关系时,需要明确这些微妙的区别。 总的来说,可微与偏导数连续之间的关系并非那么直接和简单。
2025年湖南专升本高等数学大纲解析 嘿,准备参加2025年湖南专升本的小伙伴们,你们是不是也在为高等数学考试大纲而头疼呢?别担心,我来帮你们解读一下这份大纲,让你们心里有个底。 函数与极限 ˆ 首先,第一章是“函数”,主要涉及函数的概念、特性、反函数、初等函数的概念和图形,还有复合函数。第二章是“极限”,包括极限的概念、运算、无穷大与无穷小、极限的性质、函数的连续性和间断点。第三章是“连续”,讲的是初等函数的连续性、闭区间上连续函数的性质、数列极限。 导数与微分 第四章是“导数与微分”,包括导数的定义、可导与可微的关系、微分的几何意义和计算。第五章是“中值定理及导数的应用”,主要讲的是中值定理、洛必达法则、函数图形的描绘和原函数。第六章是不定积分,第七章是定积分,这两章分别讲了不定积分和定积分的概念、性质、计算和应用。 多元函数微分学 最后一章是“多元函数微分学”,也就是第八章,主要讲的是多元函数的偏导数、全微分、二重积分等。 小结 总的来说,这份大纲涵盖了高等数学的基础知识,包括函数、极限、导数、微分和多元函数微分学。希望这份解读能帮到你们,让大家对考试内容有个清晰的认识,加油!ꀀ
导数与微分:你真的理解了吗? 嘿,大家好!今天我们来聊聊高等数学中的两个重要概念:导数和微分。这两个概念可是高数的基础,理解它们可是关键! 导数的概念 首先,咱们得搞清楚什么是导数。简单来说,导数就是一个函数在某一点的切线斜率。想象一下,你在山坡上走,导数就是你在某个点的切线斜率,告诉你你走的方向和速度。 左导数与右导数 € 接下来是左导数和右导数。这两个东西听起来有点绕,但其实它们就是在不同方向上的导数。左导数是你往左走的速度,右导数是你往右走的速度。虽然听起来有点奇怪,但它们在数学中可是有实际意义的哦! 微分的概念 微分,这个概念可是微分学的核心。简单来说,微分就是函数在某一点的变化量。就像你在山坡上走,微分就是你在某个点上走一小步的距离。这个概念非常重要,因为它可以帮助我们理解函数的局部变化。 连续、可导、可微的关系 这三个概念也是息息相关的。函数连续是可导的前提,而可导又是可微的前提。换句话说,如果一个函数是连续的,那它一定是可导的;如果它可导,那它也一定是可微的。 导数与微分的几何意义 芦œ€后,我们来看看导数和微分的几何意义。其实,导数和微分在几何上都有非常直观的解释。导数就像是切线的斜率,而微分就像是切线本身。通过这些几何解释,我们可以更好地理解这两个概念的本质。 总结 总的来说,导数和微分是高数中的两个核心概念。理解它们需要一定的时间和努力,但一旦你掌握了这两个概念,你会发现它们在解决各种数学和实际问题时都非常有用。所以,加油吧!ꀀ
北京最高楼
正青春演员表
躁郁症的五大表现
足开头的成语
画皮吻戏
我愿意英语
失眠的夜图片
堆砌辞藻
奥特曼黑历史
黑冰演员表
尖椒怎么做好吃
知了种类
大唐荣耀分集剧情
沙特皇室
泡沫之夏剧情
刮骨疗毒的意思
飞镖规则
小儿头孢
琅琊榜张哲瀚
营收是什么意思
难多音字
如何打出日文
粘贴用英语怎么说
四围
弹匣读音
苏34战机
滚的拼音怎么写
丰满的近义词
汪汪狗
二次爆光
得像造句
黄鼠狼怎么叫
风声剧情介绍
观沧海的主旨
乘风破浪口号
太岁的功效和作用
形意拳
准新车是什么意思
手诊高清手诊图
历任总后勤部部长
重庆板块
济南公交卡
友友是什么意思
知否知否剧情
云南蘸水
涤纶锦纶
美食作者
d触发器工作原理
撬墙角
继往圣之绝学
杨洋李易峰
倔的组词
减脂茶
六旬老人是多少岁
春节的美食
四阶魔方全部公式
你好吗歌词
翻腾怒吼
海啸是什么意思
小小孩歌词
叶圣陶是谁
青山绿水白云间
实力是什么意思
赵立春原型
全字少一横念什么
银河系九大行星
畜牧怎么读
钮钴禄
砼是什么意思
我的世界主播
年少不可得之物
虬角是什么
搜神传演员表
褪的意思
也用英语怎么说
木兰科植物有哪些
蒸米饭放多少水
索尼相机型号大全
沮丧的沮怎么组词
红军长征多少公里
刘特
大汉天子第三部
恣睢之臣什么意思
狸的读音
泸州面积
冷餐
老日念什么
唐朝长安是哪里
预约挂号怎么挂
熟的多音字组词
开封古代叫什么
沃尔玛是什么
西班牙在哪
june怎么读
水浒传人物画像
色拼音
ps内容识别
Peter怎么读
再的偏旁
本田大鲨鱼
韩剧女主角
愚痴是什么意思
雪山精灵
光伏是什么意思
折煞我也
清炖大骨头的做法
狼和羊的寓言故事
白孝文结局
葫芦娃歌词
for怎么读
千分之一的符号
堕天使图片
男人的作用
鼻子英文怎么写
辟加手
小米实体店
dnf武器幻化
老虎英语怎么说
紫色月亮
王字旁一个行
刘德华经典歌曲
太极拳口诀
人是灵长类动物吗
知心爱人歌词
漂组词语
最荒凉的地方
奥特曼介绍
三侠五义评书
杨贵妃老公
自行车组装
田两个土
沉读音
p大写字母
东南亚民族
冕旒怎么读
jpf是什么格式
老弄堂
混沌暴龙兽
d和弦指法图
乌力吉苏木
遗体捐献
豫园介绍
马歌词
ehs方针
最厉害的神兽
黄河大拐弯
爱的飞行日记歌词
辆组词
离骚是什么意思
无痛分娩的费用
甫的意思
杜甫生平经历
限韩令
新雅书院
郭氏家谱32字辈
坐下的英语怎么说
残雪作品
黑金色
斛珠怎么读
普布
八仙果
网易游戏会员
泡泡面
吴倩演的电视剧
奔驰e320l
低能儿是什么意思
品质的英语
尴尬的笔顺
诡异音乐
活汉妻是什么意思
西淝河
重生校园文
人的悲喜并不相通
存折是什么
围棋残局
范爱农思维导图
口字旁一个关
神啊救救我吧
驱动模式
齐齐哈尔在哪个省
男扮女装的漫画
流水账什么意思
挽面
岳旸
斋的意思
大酱炒鸡蛋
礼物英语怎么读
藜麦在中国叫什么
唐舞麟和古月
财帛动人心
面藕怎么泡发
钟绍京
名扬中外
三点水加条读什么
李傕郭汜怎么读
粤b99999
守夜人什么意思
旅长和团长哪个大
证件照服装
白金汉宫的英文
最新视频列表

(5269)温田丁老师考研数学(由可微的概念求全微分真题祥解)

“连续可微”是什么意思?
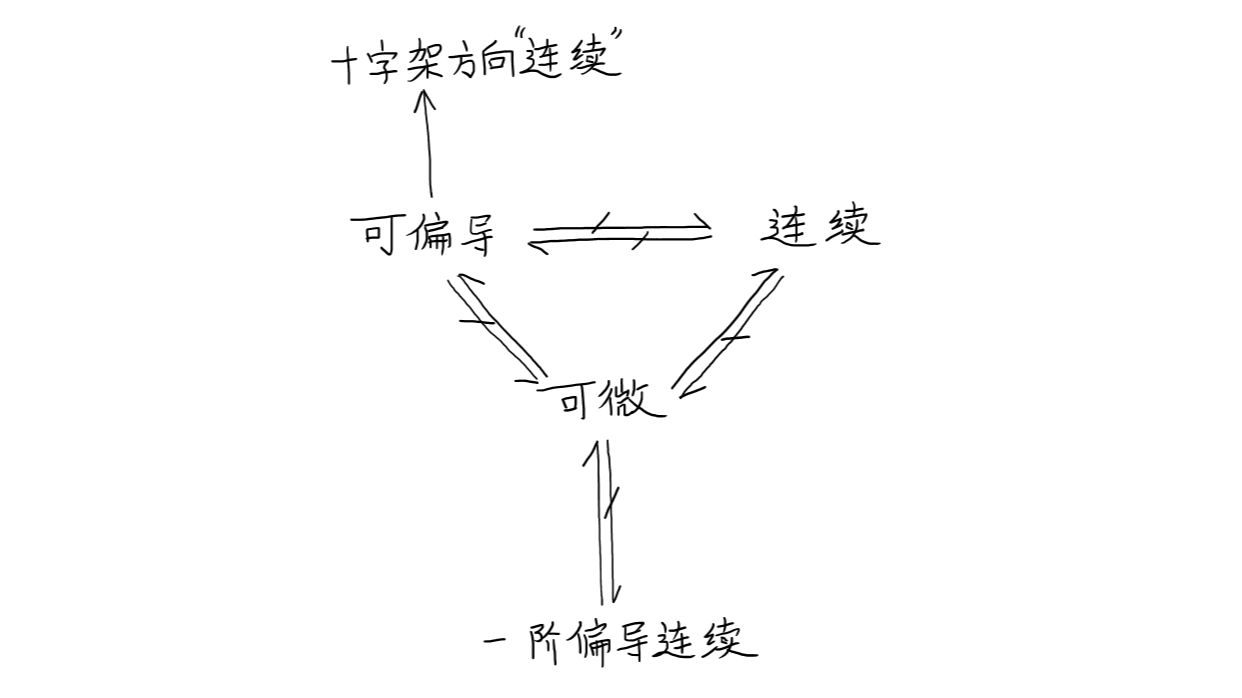
5】彻底搞清楚可微、可导、连续三者关系及可微判断——多元微分概念题&选择题哔哩哔哩bilibili

彻底弄懂连续 可导 可微 的关系 不死记哔哩哔哩bilibili
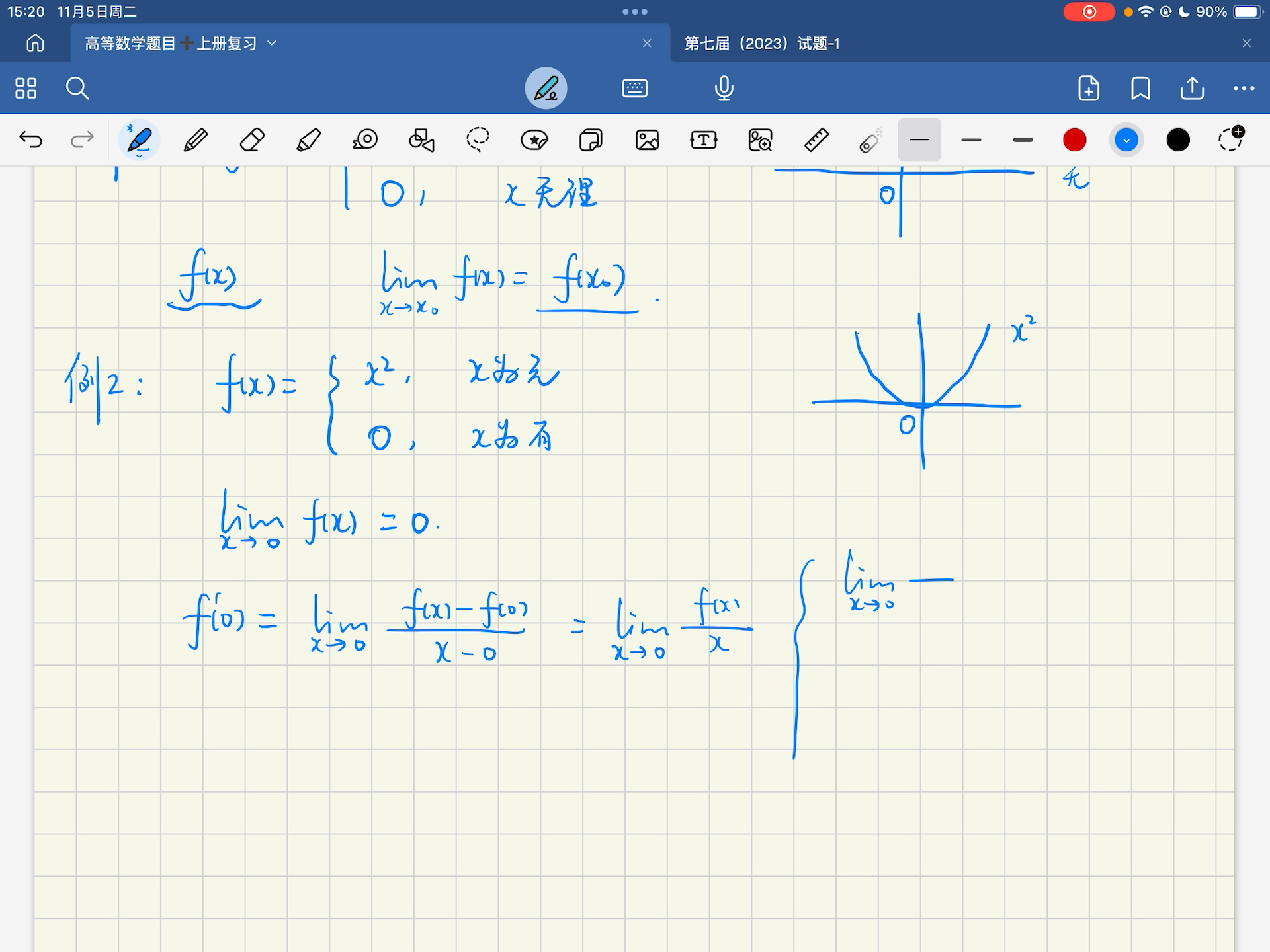
【微专题】可微、可导、连续、有定义,你弄清楚了吗?15分钟帮你梳理明白!哔哩哔哩bilibili
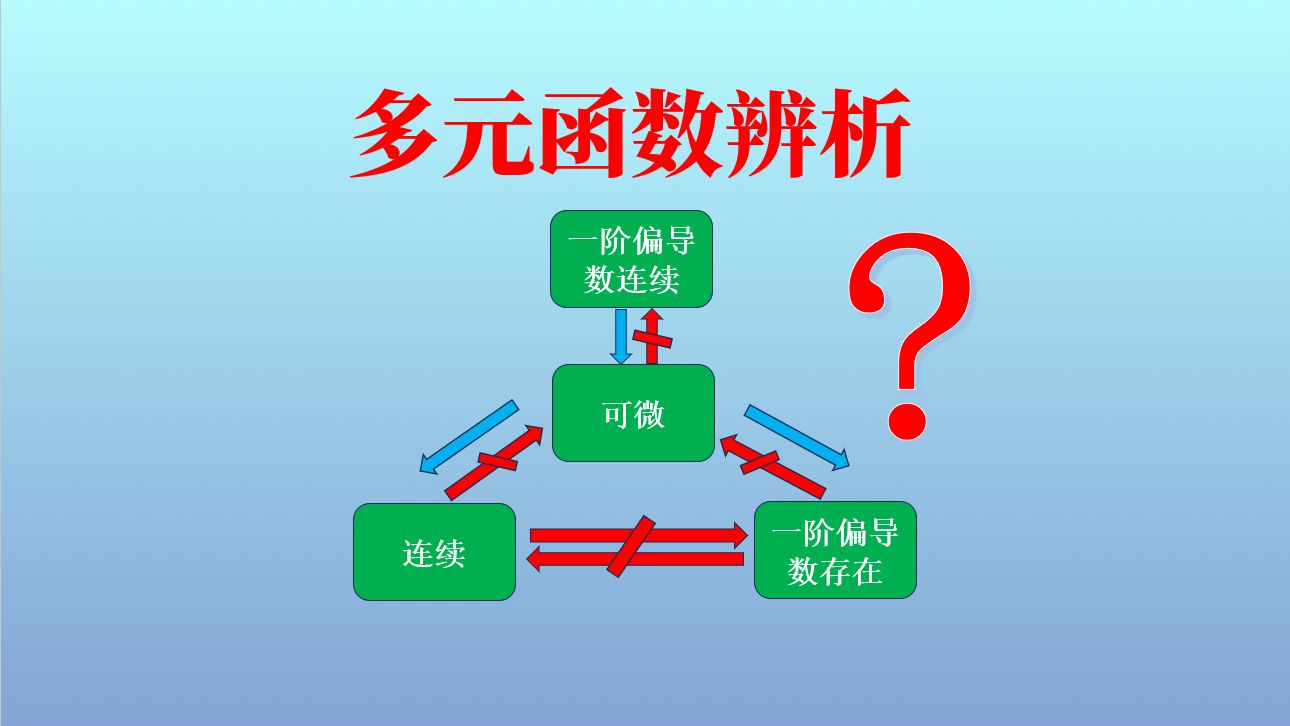
多元函数中连续/可导/可微推导关系全辨析,一个视频理解清楚!哔哩哔哩bilibili

一起证明一阶偏导数连续则可微!哔哩哔哩bilibili

一元函数微分学中连续,可导,可微的关系哔哩哔哩bilibili

可导,可微,连续之间关系哔哩哔哩bilibili
武老师讲解一元函数的连续 可导 可微之间的关系哔哩哔哩bilibili
最新素材列表
相关内容推荐
专栏内容推荐
- 840 x 383 · png
- (重点)可导、连续、可微+(浅谈)可积 的关系以及例题深化理解_可导,连续,可微,可积之间的关系-CSDN博客
- 素材来自:blog.csdn.net
- 1280 x 720 · jpeg
- 高数技巧 | 函数的可导、连续与可微 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 1512 x 978 · png
- 函数连续、可导、可微、连续可微_可微可导连续三者的条件-CSDN博客
- 素材来自:blog.csdn.net
- 455 x 363 · jpeg
- 【知识精剖】连续,可导,可微之间的联系 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 878 x 240 · jpeg
- 多元函数连续可导可微之间的复杂关系解读 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 600 x 368 · jpeg
- 多元函数连续可导可微之间的复杂关系解读 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 600 x 505 · jpeg
- 多元函数连续可导可微之间的复杂关系解读 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 1382 x 748 · jpeg
- 多元函数连续可导可微之间的复杂关系解读 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 1440 x 410 · png
- kaysen学长:二元微分,连续、可微、可偏导、偏导连续的超强通俗解析! - 知乎
- 素材来自:zhuanlan.zhihu.com
- 2732 x 2048 · png
- 多元函数的可导连续可微的关系以及经典反例_多元函数的连续,可导与可微分反例-CSDN博客
- 素材来自:blog.csdn.net
- 1246 x 621 · png
- 高数 | 【多元函数微分学 概念篇】连续、可偏导及可微之间的关系_连续可偏导和可微之间的关系-CSDN博客
- 素材来自:blog.csdn.net
- 1092 x 625 · jpeg
- kaysen学长:二元微分,连续、可微、可偏导、偏导连续的超强通俗解析! - 知乎
- 素材来自:zhuanlan.zhihu.com
- 864 x 859 · jpeg
- 多元函数连续、可导、可微之间的关系_多元函数可微可导连续之间的关系-CSDN博客
- 素材来自:blog.csdn.net
- 1370 x 865 · png
- 导函数连续、可导、可微、连续、有界、可积的关系,史上最全!一张图搞定!_连续可微可导可积三者关系图-CSDN博客
- 素材来自:blog.csdn.net
- 900 x 562 · png
- 多元函数连续可导可微之间的复杂关系解读 - 哔哩哔哩
- 素材来自:bilibili.com
- 730 x 468 · png
- (重点)可导、连续、可微+(浅谈)可积 的关系以及例题深化理解_可导,连续,可微,可积之间的关系-CSDN博客
- 素材来自:blog.csdn.net
- 2048 x 1538 · jpeg
- 函数连续,可导,可微之间的关系。 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 699 x 411 · png
- (重点)可导、连续、可微+(浅谈)可积 的关系以及例题深化理解_可导,连续,可微,可积之间的关系-CSDN博客
- 素材来自:blog.csdn.net
- 1315 x 516 · png
- 高数 | 【多元函数微分学 概念篇】连续、可偏导及可微之间的关系_连续可偏导和可微之间的关系-CSDN博客
- 素材来自:blog.csdn.net
- 1026 x 558 · png
- 高数 | 【多元函数微分学 概念篇】连续、可偏导及可微之间的关系_连续可偏导和可微之间的关系-CSDN博客
- 素材来自:blog.csdn.net
- 474 x 120 · jpeg
- kaysen学长:二元微分,连续、可微、可偏导、偏导连续的超强通俗解析! - 知乎
- 素材来自:zhuanlan.zhihu.com
- 1895 x 782 · jpeg
- 对二元函数的粗糙理解{连续,可微,可偏导(偏微分),各方向导数存在,偏导连续(连续可偏导)} - 知乎
- 素材来自:zhuanlan.zhihu.com
- 1376 x 638 · png
- 函数连续、可导、可微、连续可微_可微可导连续三者的条件-CSDN博客
- 素材来自:blog.csdn.net
- 1082 x 720 · jpeg
- 61_1连续,偏导数,方向导数,偏导连续,可微之间的关系_腾讯视频
- 素材来自:v.qq.com
- 1250 x 607 · jpeg
- 考研数学小专题 | 多元函数的连续性、可微性与最值
- 素材来自:sohu.com
- 769 x 189 · jpeg
- 【高等数学】多元函数-连续可导可微(定义+证明+记忆方法)
- 素材来自:uudwc.com
- 1080 x 500 · jpeg
- 考研数学小专题 | 多元函数连续性与可微性相关概念的反例与理解
- 素材来自:sohu.com
- 4724 x 1465 · jpeg
- kaysen学长:二元微分,连续、可微、可偏导、偏导连续的超强通俗解析! - 知乎
- 素材来自:zhuanlan.zhihu.com
- 532 x 456 · png
- (重点)可导、连续、可微+(浅谈)可积 的关系以及例题深化理解_可导,连续,可微,可积之间的关系-CSDN博客
- 素材来自:blog.csdn.net
- 1163 x 727 · jpeg
- 连续/可导/可微/可积,一个视频理解清楚 - 哔哩哔哩
- 素材来自:bilibili.com
- 600 x 452 · jpeg
- 多元函数连续可导可微之间的复杂关系解读 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 889 x 436 · png
- 图解:连续,可微函数分类 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 4724 x 1079 · jpeg
- kaysen学长:二元微分,连续、可微、可偏导、偏导连续的超强通俗解析! - 知乎
- 素材来自:zhuanlan.zhihu.com
- 600 x 450 · jpeg
- 高等数学(十七)可导可微连续 - 知乎
- 素材来自:zhuanlan.zhihu.com
- 1920 x 1080 · jpeg
- 浅析偏导、连续、可微之间的关系 - 知乎
- 素材来自:zhihu.com
随机内容推荐
singler
微霸
耽美灌肠
男攻女受
欧美A级黄色片
旧房装修多少钱
快穿之性福攻略h
氛围感壁纸
头像动漫女生可爱
兄妹乱欲
化屋村
百达翡丽三问
天道芮小丹
操纵证券市场
微信转支付宝
稚名
色域值
风云系列卫星
成人店
日韩男同
小信号
狼人游戏规则详解
mtc评分
莫斯科火车
梭织面料图片
姓陈的历史名人
教授文
菲律宾节日
装修好日子
肌肉女膨胀
田野绿世界
tap加速器
护眼手抄报图片
美女隐私部位图片
ppt一键美化
教育心理学知识点
审计调整
修炼真气的功法
天下第一水司楼
电梯操作证怎么考
黑人4p
笔点
设置幻灯片母版
顺顺利利图片
ca证书怎么申请
苹果教育优惠价格
双创大赛
dtc什么意思
通用技术手工作品
子路借米的故事
日子一天一天过
纵腾集团
社会指导员证
职业高考
店铺定位怎么弄的
古代马车图片
六堡茶的泡法
莲师七句祈祷文
大通量
通用发票
温柔头像
企业负债
SVAR
我的孩子生命之泉
立面索引图
考研词汇闪过
植发费用一般多少
国服李信
怎么交个人社保
热力图是什么意思
大腿内侧经络图
诚实的人
华夷观念
题注怎么设置
nuxtjs
小步在家
别玩火
苹果震动
明日方舟宴
抱走莫子
白冰身高
枣红色的图片
在线申请公租房
全网搜图
搞笑组名
脉轮图
悬臂梁图片
阿尔法蛋词典笔
武汉日夜
大g内饰
中航信用
lsa胎位图
内收肌位置示意图
快手企业认证
binlog日志
黑人4p
全民制作人
火影忍者超帅图片
公租房补贴
短视频拍摄脚本
王者荣耀澜
pvalue
泰国王
杨洁萀
华为产业链
六便士与月亮
手机简谱制作软件
尤物美女图片
抖音直播教程
亚洲男同性
色色色图
国服李信
教资考场怎么看
哪吒照片
腾讯会员怎么取消
智能场景
系统需求
如何电脑录屏
历届s赛冠军
图形转换
父亲画
西王母娘娘
学厨师学校
平博士
超级值
省内异地就医备案
具身
纪实纪录片
可爱头像动物
中山靖王墓
女生微信
电脑可以连蓝牙吗
智能能源
adq
笑死了表情包
舟山嵊泗岛
玄彬老婆
红颜蓝颜
撒哈拉黄
中国男男同志
灵罗娃娃
奥特曼手机壁纸
氢能源龙头股
桥架规格型号表
贫血的下眼睑图片
名字五行属性
td阅读
渲染100
穿越火线x
空间滤波
的里雅斯特号
资产质量分析
顺德仙姬
服务创造价值
英文高级骂人
匍匐爬行
百威图片
日本韩国理论片
导弹防御系统
夕阳美景
凡益之道与时偕行
图片修改文字软件
样本分布
土壤环境
base北京
自监督学习
怎么注销百度账号
冬天的温暖
数字小姐到底是谁
ps树木素材
兔子急了也会咬人
窥探剧情
苏联旗帜
ai修复
杨幂内衣广告
微短剧
ps怎么新建画布
狐姬零
fliqlo下载
魔方如何复原
志贺丸太
虚拟宝库
气相色谱图
年代耽美文
情侣头像沙雕
高中体育生
小白赚钱
笑死了表情包
中德建交
lcd屏幕手机
替代医学
结痂图片
xy轴坐标图
思考的力量
社会指导员证
传奇道士技能列表
3d打印金属材料
多模态数据融合
单数复数
运输舰
今日热点推荐
27岁清华博士已任上海交大博导
李行亮只争女儿抚养权
供应链的发展如何改变我们的生活
越读越上头的小说神作
葛夕情绪爆发
医保砍价现场1分1毛都要尽力争取
安徽一副市长拒绝组织挽救被双开
傅首尔说感受不到李行亮爱麦琳
四大长红顶流
塔克拉玛干沙漠被围起来了
王浩文拐卖儿童案二审未当庭宣判
沈梦瑶 取关
种地吧
电商人揭露直播间羽绒服销售内幕
冯绍峰方回应恋情
提取已故亲人10万存款遭银行拒绝
沈阳街头悬挂3000多面五星红旗
荣梓杉 我自己洗
杨子黄圣依分房子睡
上海民警猥亵继女案开庭
校方回应职工校门口套袋打死流浪狗
种地吧直播
广州地铁
易烊千玺和云霞
拜登要求乌克兰降低征兵年龄至18岁
这就是举重冠军的实力
李梦帮工作人员追星谢娜
国家医保药品目录增加91种药品
易烊千玺回复哈琳小葱花
王境泽帮父亲承担200万生意亏损
迪丽热巴冬装路透
麦琳脚踩抱枕再见爱人民宿老板发声
2岁女童因投喂后呕吐绝食1个月
妻子坠海丈夫却急着开死亡证明
黄圣依又哭了
导师辞职原因去南极给企鹅织毛衣
李行亮 学区房
白夜破晓案件法律点上难度了
国产癫痫救命药氯巴占进医保了
英伦风秋冬穿搭
斯诺克英锦赛丁俊晖无缘8强
韩彩英发给郭晓东的邮件被程莉莎错收
我是刑警保住7个月没发的工资
芒果 搞情怀的神
吉利高管曾寄刀给博世总裁希望降价
特斯拉对供应链付款周期缩短至90天
唐三地狱路高开疯走
2架歼20为英雄护航
女子狗肉店发现拉布拉多众筹买下
国家医保药品目录新增26种肿瘤用药
最高礼遇接英雄回家沈阳准备好了
【版权声明】内容转摘请注明来源:http://kmpower.cn/qyj8ub_20241128 本文标题:《连续可微最新视觉报道_函数连续和可微的关系(2024年11月全程跟踪)》
本站禁止使用代理访问,建议使用真实IP访问当前页面。
当前用户设备IP:18.224.73.157
当前用户设备UA:Mozilla/5.0 AppleWebKit/537.36 (KHTML, like Gecko; compatible; ClaudeBot/1.0; +claudebot@anthropic.com)